Question
Consider rolling two fair six-sided dice. Let Y be the sum of the numbers showing. What is the probability function of Y?
Answer
Author: Mohammad-Ali Bandzar| Date:Oct 15 2020
All possible outcomes from rolling 2 dice:
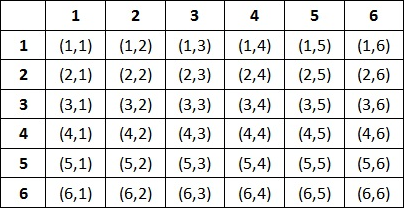
Please note that diagonals starting from any number in the left most column and going right one then up one will all have the same sum. So if we look at (5,1) it will have the same sum as (4,2),(3,3),(2,4),(1,5).
$$p\small{Y}(2) = 1/36$$ $$p\small{Y}(3) = 2/36$$ $$p\small{Y}(4) = 3/36$$ $$p\small{Y}(5) = 4/36$$ $$p\small{Y}(6) = 5/36$$ $$p\small{Y}(7) = 6/36$$ $$p\small{Y}(8) = 5/36$$ $$p\small{Y}(9) = 4/36$$ $$p\small{Y}(10) = 3/36$$ $$p\small{Y}(11) = 2/36$$ $$p\small{Y}(12) = 1/36$$ $p\small{Y}(y)=0$ for all $y\notin\{1,2,3,4,5,6,7,8,9,10,11,12\}$
All possible outcomes from rolling 2 dice:

Please note that diagonals starting from any number in the left most column and going right one then up one will all have the same sum. So if we look at (5,1) it will have the same sum as (4,2),(3,3),(2,4),(1,5).
$$p\small{Y}(2) = 1/36$$ $$p\small{Y}(3) = 2/36$$ $$p\small{Y}(4) = 3/36$$ $$p\small{Y}(5) = 4/36$$ $$p\small{Y}(6) = 5/36$$ $$p\small{Y}(7) = 6/36$$ $$p\small{Y}(8) = 5/36$$ $$p\small{Y}(9) = 4/36$$ $$p\small{Y}(10) = 3/36$$ $$p\small{Y}(11) = 2/36$$ $$p\small{Y}(12) = 1/36$$ $p\small{Y}(y)=0$ for all $y\notin\{1,2,3,4,5,6,7,8,9,10,11,12\}$