By:Mohammad-Ali Bandzar | May 2 2020
This article assumes that you understand what a Vertical Asymptote is, which you can read about Here
Up until now you've probably only learnt how to solve for vertical asymptotes graphicly, that is plotting the graph either by hand or using an online graphing calculator like desmos.com and kind of guessing where the vertical asymptotes are. Although this is a stratagey to finding vertical asymptotes it is both impractical and unreliable.
For example take the function loading... as shown below. This function kind of looks like it could have a vertical asymptote.
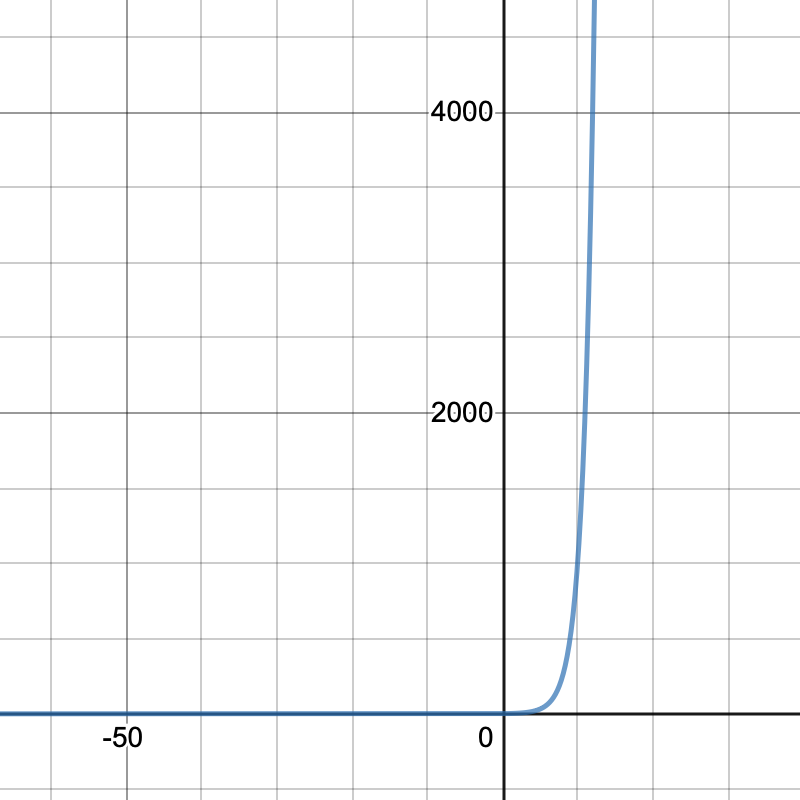
But in reality it does not, as no matter where you choose to place your vertical line representing your asymptote, if you zoom out on your graphing calculator loading... will always intersect with your line. This is because the domain of loading... is: loading... therefore it can never have a vertical asymptote as no matter where you place your vertical line the function will always intersect it.
To find vertical asymptoes within rational functions you should start by solving for when the denominator equals zero. If the denominator never equals zero then your function is likely continuous for its entire domain and has no vertical asymptotes. Once you have found the "roots" of the denominator you want to plug those numbers into the numerator and if the numerator is non-zero you have a vertical asymptote, if it is zero you have whats know as the indeterminate form loading... which represents a hole in the function.
We can see that the graph approaches but never reaches x=0 as shown with the dashed line:
We can then solve for the equation of this vertical asymptote by solving for when the denominator of the function is equal to zero, in this case it is zero. We then want to label our asymptote at the bottom of the page next to the asymptote with its equation.
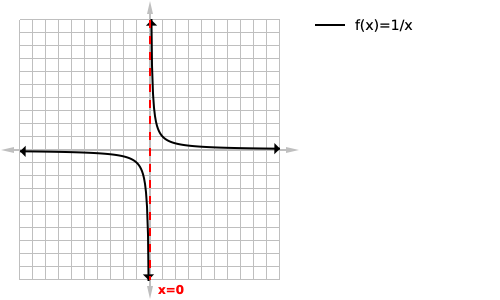
We want to start off by solving for when our denominator is equal to zero:
loading...
loading...
We then want to plug this into our numerator and see what the result is:
loading...
loading...
loading...
Since the numerator is zero, we can conclude that this is not a vertical asymptote but instead a hole as shown in the image below(where the circle represents the hole in our function):
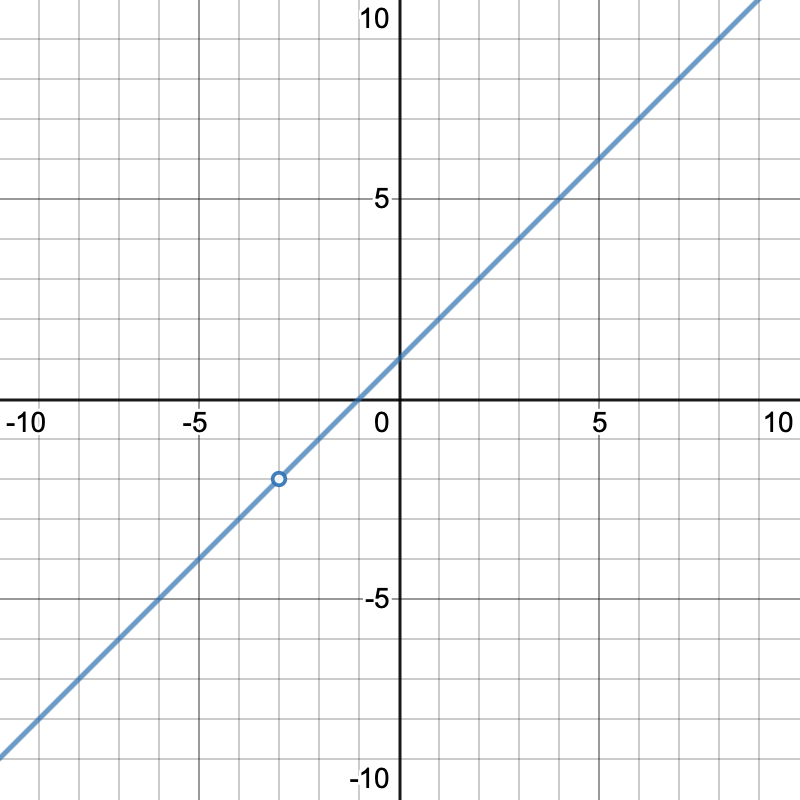
This could have also been determined by either graphing, plugging in numbers close to where you believing the asymptote would be and recognizing that it isnt going toward infinity as demonstrated in the table above, or by seeing that the numerator and denominator have the same factor and canceling those out as follows:
loading...
loading...
loading...
loading...
has no real solutions telling us that the function will not have any vertical asymptotes.
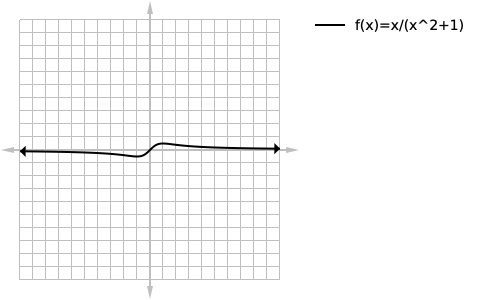
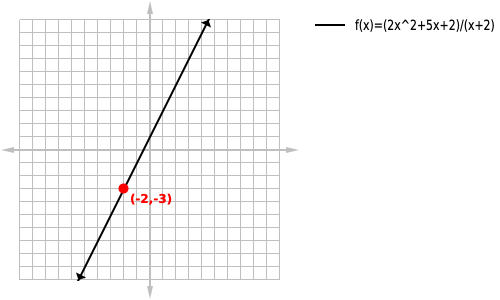
We will start by solving for when the denominator is equal to zero.
loading...
loading...
We are then going to plug -2 into our numerator and see what we get:
loading...
loading...
loading...
loading...
since the numerator is zero, we can conclude that this is not a vertical asymptote but instead a hole as shown on the graph below:
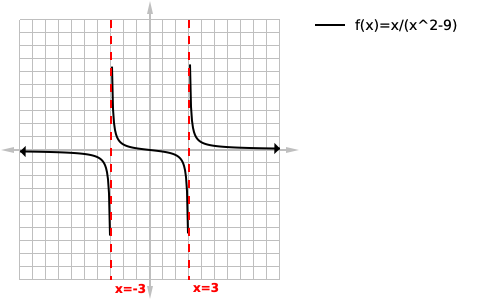
We will start off by setting the denominator equal to zero and solving:
loading...
loading...
loading...
loading...
We are then going to plug -3,+3 into our numerator and see what we get:
we get -3,+3 since neither of these are zero we can conclude that our function will have two vertical asymptotes one at -3 and one at +3:
We will start off by setting the denominator equal to zero and solving:
loading...
loading...
for any integer value of k. that is this function has infinite many zeros and they are all the multiples of pi.
Since we cant realistically plug in infinite many values into our numerator, we will instead find the zeros of our numerator and compare the two
loading...
loading...
since both our numerator and denominator have a zero when loading... we can conclude that that will be a hole in our function and that our vertical asymptotes will be all the other zeros of our denominator.
Therefore our vertical asymptotes are at the following locations:
loading... where k is any integer not equal to one
and our only hole will exist at loading...
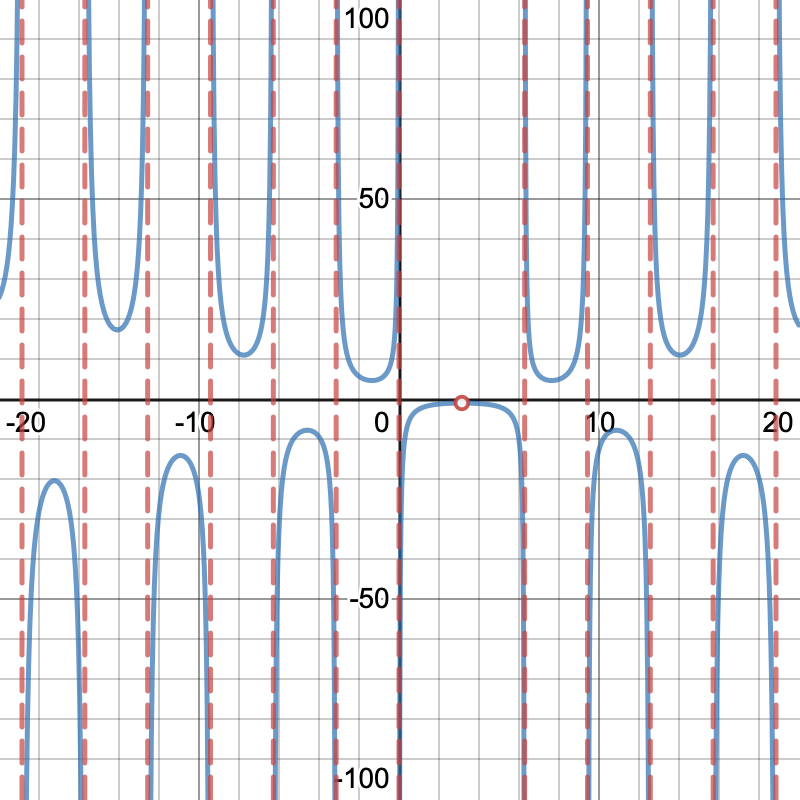
Some trig functions will also have their own vertical asymptotes such as loading... which has infinite many vertical asymptotes loading... where k can be any integer. If you ever forget you could always remember that loading... and try to solve that as demonstrated above.
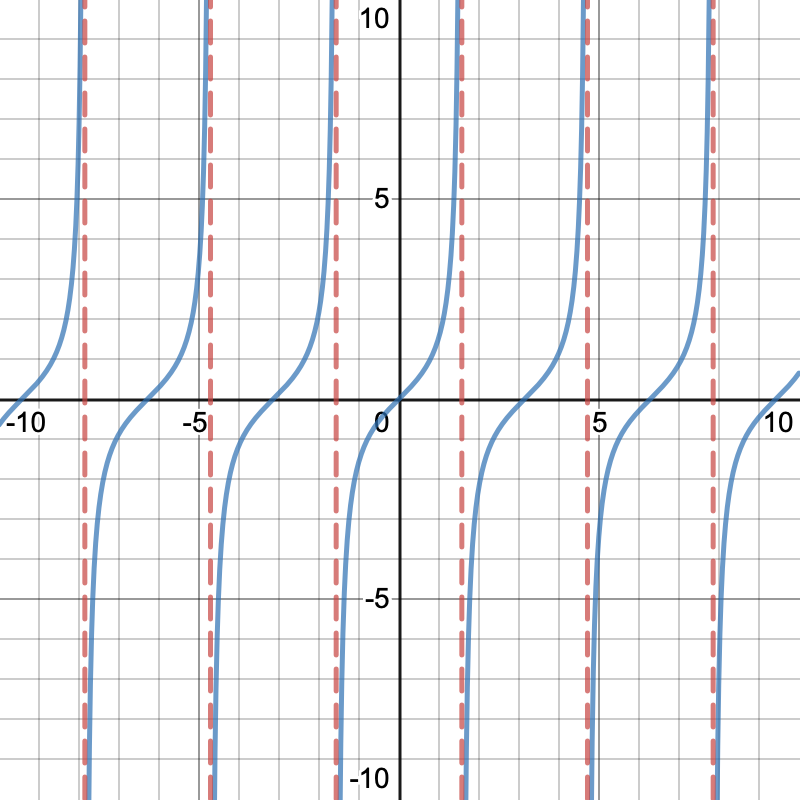
Many other trig functions such as all the reciporcal ones loading... But these are all fairly easy to solve as long as you think of them as rationals and follow the steps shown above
- Make youself comfortable solving quadratic and cubic equations and factoring
- Don't forget to verify that the zero in the denominator is in fact an asymptote
- Don't forget that some functions like loading... have an infinite number of vertical asymptotes
- Use a graphing calculator/desmos.com to verify your solutions
THANKS FOR READING